コイルと直交する棒磁石を時間的に変化させる場合を考えます。この磁石を鉛直方向に移動させると、その移動中 のみ電圧e[V]が誘起されます。これが誘導起電力です。
この際生じる電圧の向きは、磁束が増加するとき(N極を近づけるとき)はその磁束の増加を妨げる (つまり減少させようとする)磁束が発生するように電圧が誘起され、減少するとき(N極を遠ざける)はその磁束の減少を妨げる(つまり増加させようとす る)磁束が発生するように電圧が誘起されます。
これを数式で表現すると以下のようになります。
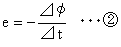
磁束の変化を連続的に起こし、常時誘導起電力を生じさせる場合、交流電源を用いることを考えます。
いま、コイル1とコイル2の間には交流電源E[V]により生じる磁束φがあり、コイル1とコイル2両方に鎖交しています。その磁束には⊿t[s]の時間変化当たり⊿φ[Wb]の変化が生じています。またコイル2を鎖交する磁束φ2はコイル1を流れている電流I1[A]に比例することから
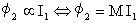
となります。これにより、コイル2の端子に生じる誘導起電力e[V]は②式から
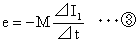
となり、このときの誘導作用をとくに相互誘導、M[H]を相互インダクタンスといいます。このM[H]はコイル1とコイル2の巻き数の比やコイルと鎖交す る磁束が通る磁路の媒質により定まる定数で、誘導起電力の生じやすさの程度を示す量です。
また、コイル単体に対して交流電源を接続した場合に対しても誘導作用が起こり、これを自己誘導といいます。
このとき定義されるL[H]を自己インダクタンスといい、次式が成り立ちます。
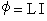
よって②式より
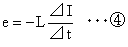
自己インダクタンスも相互インダクタンス同様にコイルの巻き数や内部の媒質により定まる量です。